三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简深圳市某某系统技术维修站目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简深圳市某某系统技术维修站考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
(责任编辑:综合)
-
 关于草莓这些“传言”是真的吗2025-12-15 09:04:54 来源:重庆晨报 作者:刘湃
...[详细]
关于草莓这些“传言”是真的吗2025-12-15 09:04:54 来源:重庆晨报 作者:刘湃
...[详细]
-
 7月25日消息,今日晚间,东方甄选在港交所公告,7月25日,董宇辉买方)、北京新东方迅程网络科技有限公司卖方)及与辉同行北京)科技有限公司目标公司)订立出售协议,据此,卖方同意出售,而买方同意收购目标
...[详细]
7月25日消息,今日晚间,东方甄选在港交所公告,7月25日,董宇辉买方)、北京新东方迅程网络科技有限公司卖方)及与辉同行北京)科技有限公司目标公司)订立出售协议,据此,卖方同意出售,而买方同意收购目标
...[详细]
-
 #雅安暴雨山洪仍有25人失联#[#雅安暴雨山洪已致14人遇难#]记者从四川雅安汉源县马烈乡“7·20”山洪泥石流灾害抢险救援指挥部获悉,截至今天14时30分,已搜寻到遗体14具,仍有25人失联,搜
...[详细]
#雅安暴雨山洪仍有25人失联#[#雅安暴雨山洪已致14人遇难#]记者从四川雅安汉源县马烈乡“7·20”山洪泥石流灾害抢险救援指挥部获悉,截至今天14时30分,已搜寻到遗体14具,仍有25人失联,搜
...[详细]
-
 当地时间22日上午,加沙地带中部代尔拜拉赫的一家医院遭到以军空袭,造成至少1人死亡、2人受伤。据悉,死者为一名记者。 视频拍摄者:谁去拿个灭火器过来?灭火器,伙计们,灭火器。刚才,阿克萨医院的记
...[详细]
当地时间22日上午,加沙地带中部代尔拜拉赫的一家医院遭到以军空袭,造成至少1人死亡、2人受伤。据悉,死者为一名记者。 视频拍摄者:谁去拿个灭火器过来?灭火器,伙计们,灭火器。刚才,阿克萨医院的记
...[详细]
-
 2024年的暑假,最火的是“大女主”三个字。暑期档最火的三部剧:黄亦玫,在《玫瑰的故事》里爱得起放得下,在任何时刻都坚定地遵从自我。薛芳菲,《墨雨云间》女主,绝不内耗,主打一个敢爱敢恨睚眦必报。在夏天
...[详细]
2024年的暑假,最火的是“大女主”三个字。暑期档最火的三部剧:黄亦玫,在《玫瑰的故事》里爱得起放得下,在任何时刻都坚定地遵从自我。薛芳菲,《墨雨云间》女主,绝不内耗,主打一个敢爱敢恨睚眦必报。在夏天
...[详细]
-
“男子被流浪猫绊倒投喂者赔24万元”案再审宣判:公司承担80%,投喂者20%
 原标题:“男子被流浪猫绊倒投喂者赔24万元”案再审宣判:公司承担80%,投喂者20%) 7月24日,“男子被流浪猫绊倒投喂者赔24万元”案再审宣判。6月5日上午,
...[详细]
原标题:“男子被流浪猫绊倒投喂者赔24万元”案再审宣判:公司承担80%,投喂者20%) 7月24日,“男子被流浪猫绊倒投喂者赔24万元”案再审宣判。6月5日上午,
...[详细]
-
 第三十三届奥运会中国体育代表团22日抵达巴黎,团部工作人员表示一切顺利。 22日18时许,巴黎奥运会中国体育代表团从北京飞抵巴黎。国家体育总局局长、中国体育代表团团长高志丹及团部工作人员顺利抵达
...[详细]
第三十三届奥运会中国体育代表团22日抵达巴黎,团部工作人员表示一切顺利。 22日18时许,巴黎奥运会中国体育代表团从北京飞抵巴黎。国家体育总局局长、中国体育代表团团长高志丹及团部工作人员顺利抵达
...[详细]
-
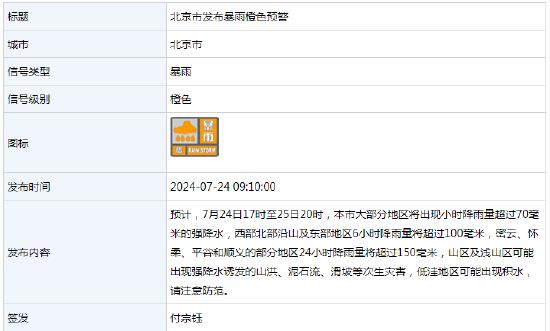 来源:北京市气象局 预计,7月24日17时至25日20时,本市大部分地区将出现小时降雨量超过70毫米的强降水,西部北部沿山及东部地区6小时降雨量将超过100毫米,密云、怀柔、平谷和顺义的部分地
...[详细]
来源:北京市气象局 预计,7月24日17时至25日20时,本市大部分地区将出现小时降雨量超过70毫米的强降水,西部北部沿山及东部地区6小时降雨量将超过100毫米,密云、怀柔、平谷和顺义的部分地
...[详细]
-
NASA准局长称“要在中国前重返月球”?中方多次表态:无意搞太空竞赛
 来源:环球时报【环球时报特约记者 王逸】被美国总统特朗普提名出任美国国家航空航天局NASA)局长的贾里德·艾萨克曼将于当地时间3日参加国会参议院提名确认听证会,阐述与中国的登月竞赛以及深空探索计划。据
...[详细]
来源:环球时报【环球时报特约记者 王逸】被美国总统特朗普提名出任美国国家航空航天局NASA)局长的贾里德·艾萨克曼将于当地时间3日参加国会参议院提名确认听证会,阐述与中国的登月竞赛以及深空探索计划。据
...[详细]
-
 新消费日报 7月24日讯,今日新消费日报的主要内容有:滴滴出行出租车的夜间需求相比5月上涨36%;橡鹿科技旗下AI炒菜机器人上线煤油检测功能;贵州茅台称下半年是渡过本轮行业调整的关键期。行业要闻农夫山
...[详细]
新消费日报 7月24日讯,今日新消费日报的主要内容有:滴滴出行出租车的夜间需求相比5月上涨36%;橡鹿科技旗下AI炒菜机器人上线煤油检测功能;贵州茅台称下半年是渡过本轮行业调整的关键期。行业要闻农夫山
...[详细]

 悉尼邦迪海滩枪击13人被送医
悉尼邦迪海滩枪击13人被送医 中国癌症高发,是吃太多食品添加剂惹的祸?提醒:少碰6种添加剂
中国癌症高发,是吃太多食品添加剂惹的祸?提醒:少碰6种添加剂 以军袭击约旦河西岸多地 造成至少7人死亡
以军袭击约旦河西岸多地 造成至少7人死亡 法院通报辽B公务车多次恶意插队别车
法院通报辽B公务车多次恶意插队别车
